I am not really a fan of Al Khwarizmi, I never understood Algebra, and I never approved the algorithmic approach in the first place. In fact, I wish I could wipe this guy’s names out of the books of history, since all what the guy did sounds like a pure scam to me: copy Greek logic and reintroduced it differently! Personally spoken, I always found pure logical approaches extremely intuitive, as opposed to algorithmic and algebraic approaches.
It should be noted that science is cumulative, that the Greeks themselves must have built their knowledge on top of previous, existing knowledge, and that pure reinterpretation without any proper attribution is nothing but pure plagiarism.
Nevertheless, throughout this blogpost, I will be explaining the concept of algorithm and the justifications behind the use of the algorithmic approach. I will start with a couple definitions, followed by the justifications, and end with an alternative definition that exposes the nature of the algorithm.
Definitions
For the purpose of the blogpost, a couple definitions are in place. The definitions are aimed at illustrating an overlap between two concepts: the concept of algorithm, and that of the flowchart. Throughout the blogpost, both terms may be used interchangeably.
Algorithm
“An algorithm is a sequence1 of steps towards achieving a certain goal. At each step of the sequence, a certain instruction is issued, which may be related to input/output operations, data processing operations, or control flow.”
Code Snippet 1 demonstrates the pseudocode for one algorithm that calculates the length of the full name given two input values: the first name, and the last name. Code Snippet 2 demonstrates the code for the equivalent Python function. Code Snippet 3 demonstrates the code for the equivalent Java function. Never mind the extra tokens for the moment: the try (...) clause, the throws ... declaration, and the curly braces.
calculate_full_name_length:
output "please provide your first name..."
input first_name
output "please provide your last name..."
input last_name
first_name_length = len(first_name)
last_name_length = len(last_name)
total_length = first_name_length + last_name_length
output "the length of your full name in characters is..."
output total_length
returnCode Snippet 1: Calculate full name length.
def calculate_full_name_length():
print("please provide your first name…")
first_name = input()
print("please provide your last name…")
last_name = input()
first_name_length = len(first_name)
last_name_length = len(last_name)
total_length = first_name_length + last_name_length
print("the length of your full name in characters is…")
print(total_length)
returnCode Snippet 2: Python function that calculates the length of the full name. The return statement is optional.
public static void calculate_full_name_length() throws IOException {
try (LineNumberReader reader = new LineNumberReader(new InputStreamReader(System.in))) {
System.out.println("please provide your first name…");
String first_name = reader.readLine();
System.out.println("please provide your last name…");
String last_name = reader.readLine();
int first_name_length = first_name.length();
int last_name_length = last_name.length();
int total_length = first_name_length + last_name_length;
System.out.println("the length of your full name in characters is…");
System.out.println(total_length);
}
return;
}Code Snippet 3: Java function that calculates the length of the full name. The return statement is optional.
Flowchart
“A flowchart is a set of interconnected nodes. Each node in a flowchart has a certain shape that denotes the specific function carried out by the node: signal the start or end of the flowchart, input/output operation, data processing operation, or control flow. Each node is connected to at least one other node by means of a one way connection.”
Figure 1 demonstrate a flowchart visualising the algorithm that calculates the length of the full name given two input values: the first name, and the last name. Compare the nodes in the flowchart with the steps in the algorithm demonstrated in Code Snippet 1, and note the total overlap.
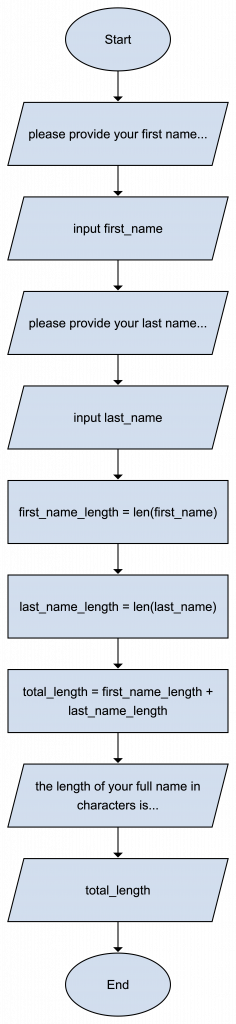
Figure 1: Calculate full name length. Made with yEd Live.
Cognition
It is argued in some circles that the natural way of thinking is algorithmic, meaning that the individual must devise a certain algorithm in order to achieve a goal and/or accomplish a task. This supposed natural way of thinking may arguably be noticed in all aspects of human life: home, in school, and at work. In fact, in academic settings and commercial environments, the flowchart is the primary means by which scholars and professionals visualise their arguments. Moreover, specific instructions in these settings are always provided by means of sequences of instructions.
For instance, when thirsty, the individual must apply an algorithm to reach the kitchen and drink water, which may start with the action of the person standing up on their feet as the first step in the algorithm, followed by the action of the person turning towards the door, succeeded by the action of the person walking towards the door, then, the action of the person checking whether the door is closed to open the door in which case, walking past the door, and so on, until the person reaches the water tap and fills a glass of water and drinks the water. This is a basic illustration of where and when an algorithm may be applied: home.
Additionally, scholars often resort to models instead of theories to account for a certain phenomenon. For instance, Fromkin (1971) summarised the findings of one research by means of a certain diagram that resembles a flowchart, and which may be said to be a rough approximation of a certain algorithm that is employed for the purpose of speech production. Aside from the fact that the diagram occurs in a certain scientific context, and as in the case of the many models proposed in the field of psychology, the model proposed by Fromkin presumes that algorithms are employed in the psychological realm. Therefore, the models confirm that algorithms are everywhere around us, since human conception is algorithmic in nature.
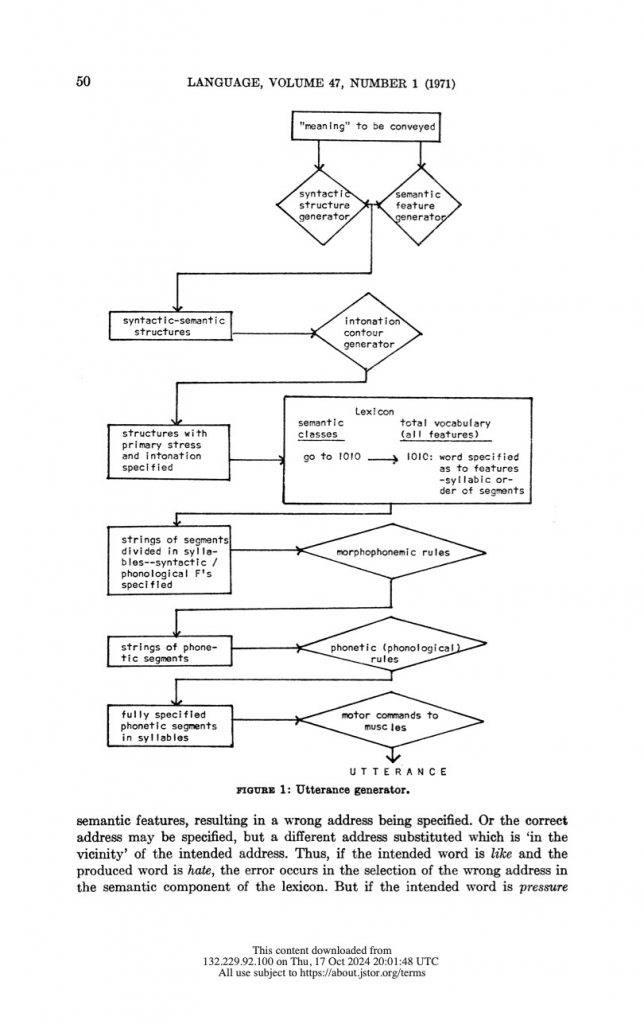
Figure 2: Speech production model (Fromkin, 1971).
Moreover, the flowchart is a popular tool among business personnel. It is a common practice in commercial environments to visualise all kinds of processes by means of flowcharts. These processes may be sales related, production related, resource or asset management related, etc.
Now that the reader has just realised that they are just a robot, since, according the previous claims, the reader thinks, acts and behaves like robots, it should be noted that the art of computing,2 like all arts, is all about self expression, and that computer engineers, like all artists, are constantly seeking self expression. Consequently, it may be said that the computer is another form of depicting human nature. Indeed, some parts of the computer are designed to depict some functions of the brain. The RAM, for instance, stands for the short term memory. The hard disk, in another instance, stands for the long term memory. The ALU depicts certain skills that humans acquire at school: arithmetic and logic processing. Furthermore, the division between hardware and software corresponds to the division between brain/neurology and mind/psychology, respectively. (Or the division between body and soul in some ultra conservative, boring circles.) This self expression further proves the claim that the reader is nothing but a robot.
Logic
Note that the definition of algorithm above, like all the definitions that I came across, overlooks some important aspects of the algorithm: what is a step? and what is the nature of the relation between two consecutive algorithmic steps?
During my career, I experimented a lot with programming languages, and I tried to employ some of the most unusual paradigms in commercial settings, which might have caused lots of inconveniences among mediocre programmers, the programmers that are found in small, medium, and large businesses. Eventually, I discovered a method to transform an algorithm into a purely logical, mathematical formula, which further proves that an algorithm is nothing but a logical, mathematical expression. Based on my humble experience, I propose the following alternative definition of the algorithm.
“An algorithm is a sequence of nested functions. Each step in the algorithm, that is a function, is composed to the function that is the immediately succeeding step in the sequence. Consequently, each step in the algorithm is a function that defines a scope into which all the succeeding steps fall. “
Obviously, unlike traditional definitions of the algorithm, the proposed alternative definition does not overlook the nature of the algorithmic step and the relation between two consecutive algorithmic steps. Moreover, the alternative definition provides the first step towards a total paradigm shift: from the structured/imperative programming paradigm, to the functional/declarative programming paradigm.3
Code Snippet 4 demonstrates one lambda expression that calculates the length of the full name. Note the sequence of λ<parameter-name> at the beginning of the expression, which denote a series of function compositions. Code Snippet 5 demonstrates the code for the equivalent Python lambda expression.4
(λignore1.
(λfirst_name.
(λignore2.
(λlast_name.
(λfirst_name_length.
(λlast_name_length.
(λtotal_length.
(λignore3.
output total_length
)(output "the length of your full name in characters is...")
)(first_name_length + last_name_length)
)(len(last_name))
)(len(first_name))
)(input)
)(output "please provide your last name...")
)(input)
)(output "please provide your first name...")Code Snippet 4: Lambda expression that calculates the length of the full name.
(lambda ignore1:
(lambda first_name:
(lambda ignore2:
(lambda last_name:
(lambda first_name_length:
(lambda last_name_length:
(lambda total_length:
(lambda ignore3:
print(total_length)
)(print("the length of your full name in characters is..."))
)(first_name_length + last_name_length)
)(len(last_name))
)(len(first_name))
)(input())
)(print("please provide your last name..."))
)(input())
)(print("please provide your first name..."))Code Snippet 5: Python function that calculates the length of the full name, written in functional programming style, the best style!
Conclusion
Obviously, Al Khwarizmi’s name will remain stuck in the books of history, since algorithms are being used everywhere. Although, the nature of the algorithm is still obscure, given the primitive definitions widely available. Moreover, ignoring algebra for the moment and the origins of which, algorithms do not provide any additional value, except for being incompatible with mathematics. Yet, algorithms are still considered as being exactly mathematical.
Nevertheless, due to the supposed simplicity of the algorithmic approach, most readers may opt for an algorithmic interpretation of some phenomena, a choice that a seasoned mathematician5 may never opt for. In contrast, mathematicians tend to reconstruct the universe in terms of pure logical constructs, like sets and lambda functions. In fact, most mathematicians, if not all, would go far and claim that everything is a set or everything is a function depending on their personal preferences. In either case, the transition between sets and functions, like the transition between algorithms and functions as demonstrated earlier, is a simple matter, rendering the question of whether everything is a set or a function redundant.
Due to the nature of the algorithm that is error prone, I personally prefer to stick to basic logical constructs. Based on my experience, writing programs in the functional programming style results in fewer errors. In contrast, writing an algorithm is a very risky task, and the programmer may commit a mistake at any place in the code easily. Moreover, the algorithmic approach may result in regions in the code that do not meet the requirements of a function, whereas functional programming style is fully compatible with mathematics.
A final remark. If I ever thad the chance, like if I become the dictator of planet Earth, I would totally abandon the algorithmic approach that is being employed everywhere, I would forbid all citizens of planet Earth from ever writing an algorithm, and I would force every single programmer to write in the functional programming style, the best style ever!
References
Fromkin, V. A. (1971). The Non-Anomalous Nature of Anomalous Utterances. Language, 47(1), 27. https://doi.org/10.2307/412187
Notes
- As in the case of the various terms employed in this blogpost, the choice of word “sequence” is not arbitrary. See the mathematical definition of sequence for further clarification. ↩︎
- In fact, it is neither art nor science. It is a craft! A considerable number of programmers that I have met do not even hold a degree, whether computing related or not. ↩︎
- The latter is more polite by the way, since the programmer declares an intention, or asks a question. Whereas, in the former case, the programmer is being bossy and constantly provides a series of instructions to the computer. ↩︎
- Due to the nature of Java, which is way more strict than Python, writing the same function in functional programming style requires a few additions, rendering the example incompatible with the algorithm from Code Snippet 1 and the lambda expression from Code Snippet 4. Therefore, no Java equivalent is presented. Moreover, the strict nature of Java may be said to have revealed a flow in the algorithmic approach, since some functions are procedures, that is, they do not return any value, which contradicts the formal definition of a function. ↩︎
- Which I am not by the way. Although, I tend to include many mathematical concepts in my arguments. ↩︎



Recent Comments